Methods for Solving Limits with Explanations, Practice Questions, and Answers [AP Calculus, Calculus 101, Math] – Moosmosis

In this article, we will talk about the methods for actually solving or evaluating limits. There are practice questions included, labeled PRACTICE, and they are there for you to test your understanding of the different methods. The answers are at the very bottom. Enjoy!

Method 1: Direct Substitution

The first method you should try when given a limit is direct substitution. This is by far the easiest of the methods for analyzing limits, and can save a lot of time. All you need to do is simply plug the desired x-value into the expression.

In other words, you can use this property:

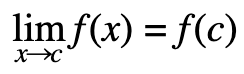
For instance, say you wanted to evaluate the limit as x approaches 2 of 2x + 3. This could be written as

To evaluate this, you could simply plug 2 into the expression 2x + 3, and you would get 7 as your answer.

Here’s one that would require a little more thought.

Evaluate the limit as x approaches 0 of 1/x².

When we try plugging in 0 for x, we get 1/0, which is clearly undefined. Uh oh, we’re stuck. Well, not really – we can look back to our study of infinite limits to help us. If we think about taking smaller and smaller values of x, the denominator, x², gets smaller and smaller, getting super close to 0. Therefore, our expression 1/ x² takes on larger and larger positive values without bound, generating a vertical asymptote. Noting that the left and right limits are the same, we can say:

Important!

As always, the left- and right- sided limits must be equal for the double-sided limit to exist. Don’t forget this as you explore more complicated methods for evaluating limits!

Clearly direct substitution is quick and easy, so you may wonder why we cannot always use it. Take a look at the following problem:

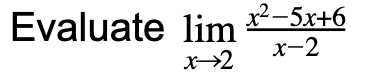
Trying our substitution tactic again, we find that the limit evaluates to 0/0. So, we conclude that, just like in the problem above, the limit evaluates to positive or negative infinity, right? WRONG!

When we were looking at 1/x² as x approached 0, direct substitution told us that our limit evaluated to 1/0, and from this we were able to conclude that there was an asymptote. We were able to do this, because the numerator was a nonzero constant value, namely 1, and thus even as our denominator kept getting smaller and smaller, our numerator did not change.

However, in this example, our limit evaluated to 0/0, and thus we don’t actually know whether our function is going to blow up to a very large or small number. We also cannot conclude that the limit is equal to 1, because 0/0 is undefined. For all we know, our numerator and denominator could have approached 0 at the same or different rates, and we must use more advanced methods to evaluate the limit.

PRACTICE

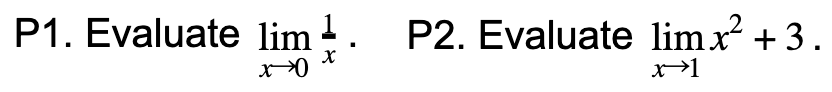
Method 2: Factoring

Factoring can be very useful when evaluating funky limits like the one we saw above, where we got 0/0 as our answer. In fact, if you ever get 0/0 as an answer and you are taking the limit of a rational function, there is a good chance you will need some kind of factoring to help you out. Recall that a rational function is a ratio of 2 polynomials (the one in the denominator should be nonzero).

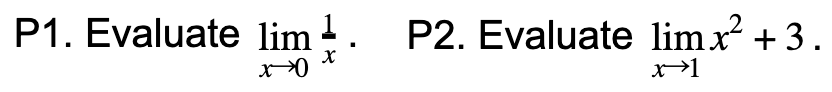
Let’s take another look at the problem from earlier.

We know that simple substitution results in 0/0, so this time, we factor the numerator in hopes of finding some terms that cancel. Fortunately, we are not disappointed.

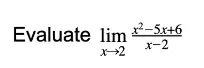
We can now cancel the (x-2) term that appears in the numerator and denominator, which gets rid of our division-by-zero we had earlier. Now we can finish with substitution.

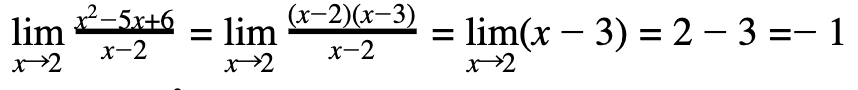
Now you try.

PRACTICE

Method 3: Conjugates

Sometimes, substitution and factoring do not work, and you will need to find an alternative solution. If you see a bunch of radical symbols in the expression you need to take the limit of, you may want to consider using conjugates. By multiplying the numerator and denominator of an expression by the conjugate of a radical expression, you can create factors that cancel and a nicer looking expression. Remember that since you are multiplying the numerator and denominator by the same thing, you are really just multiplying the entire expression by 1.

For instance, say you wanted to evaluate the following:

Simple substitution yields 0/0 which we know we don’t want, and it’s unclear how we would factor this expression (although there is a way to factor the numerator, and I would encourage you to try it). Seeing a radical in the denominator, we multiply by the conjugate of our denominator. We then use difference of squares to clean up our denominator and cancel the common factor of (x-1).

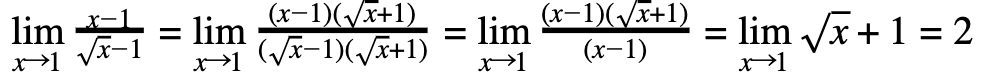
Notice that we just used direct substitution at the end to finish it up.

Important!

This example demonstrates the general method for evaluating limits of expressions with radicals in the numerator or denominator.

1. Multiply the numerator AND denominator by the conjugate of the numerator OR denominator (depending on which one has the radical expression)
2. Simplify using difference of squares
3. Cancel common factors
4. Use substitution to evaluate

PRACTICE

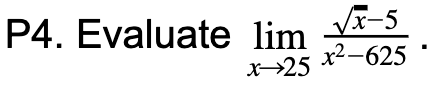
ANSWERS

P1. Does not exist (DNE); the left and right sided limits don’t match up

P2. Substitute 1 into the expression to get 4

P3. Factor the numerator, cancel the (x-4) term, and use substitution to get 4

P4. Multiply the numerator and denominator by the conjugate of the expression in the numerator, factor the denominator using difference of squares, cancel the (x- 25) term, and substitute x = 25 into the expression to get 1/500

Click and check out these popular articles for more information: 🙂

Calculus: Two Important Theorems – The Squeeze Theorem and Intermediate Value Theorem

Calculus: Limits and Continuity

Ectoderm vs Endoderm vs Mesoderm

Psychology 101 and the Brain: Stress – Definition, Symptoms, and Health Effects of the Fight-or-Flight Response

Circulatory System: Blood Flow Pathway Through the Heart

Circulatory System: Heart Structures and Functions

Ductus Arteriosus Vs Ductus Venosus Vs Foramen Ovale: Fetal Heart Circulation

Cardiac Arrhythmias: Definition, Types, Symptoms, and Prevention

Upper Vs Lower Respiratory System: Upper vs Lower Respiratory Tract Infections

Seven General Functions of the Respiratory System

Digestive System Anatomy: Diagram, Organs, Structures, and Functions

Kidney Embryology & Development: Easy Lesson

Psychology 101: Crowd Psychology and The Theory of Gustave Le Bon

Introduction to Evolution: Charles Darwin and Alfred Russel Wallace

Symbolism of Shoes in Dreams



Support Us at Moosmosis.org!

Thank you for visiting, and we hope you find our free content helpful! Our site is run 100% by volunteers from around the world. Please help support us by buying us a warm cup of coffee! Many thanks to the kind and generous supporters and donors for doing so! 🙂

 Copyright © 2022 Moosmosis Organization: All Rights Reserved

All rights reserved. This essay first published on moosmosis.org or any portion thereof may not be reproduced or used in any manner whatsoever
without the express written permission of the publisher at moosmosis.org.

Please Like and Subscribe to our Email List at moosmosis.org, Facebook, Twitter, Youtube to support our open-access youth education initiatives! 🙂